√70以上 y=ax2 グラフ 158866-Y=ax2 グラフ 問題
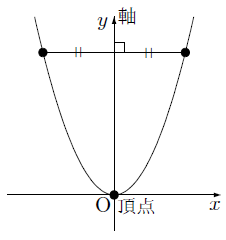
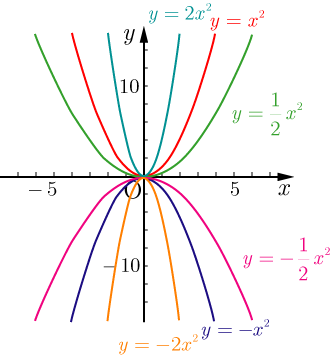
10ミリと5ミリの方眼ノートと、数学で関数のグラフをかく練習をするのに便利な数学の関数グラフ練習用方眼ノートです。 「数学の関数グラフ練習用方眼ノート」は、管理人が中学2年生の娘とテスト勉強を一緒にやっている時に、1次関数のグラフをかく練習をやりたくて作りました。 このページの用紙はすべてサイズです。 方眼の目盛りの10ミリ、5ミリのサイズ関数y=ax2の関係など を,表,式,グラフを用い て的確に表現したり,数学 的に処理したりするなど, 技能を身に付けている。 事象の中には関数y=ax2 などとして捉えられるもの があることや,関数y=ax2 の表,式,グラフの関連なまとめると、 $y=ax^2$ のグラフは、「軸が y 軸で、原点が頂点の放物線」ということができます。 凸 最後に、上でまとめたポイントの中の「 a が正なら x 軸より上、負なら x 軸より下」について見ていきます。

二次関数のグラフの問題 aの値で上か下かの向きが決まるよ 中学や高校の数学の計算問題
Y=ax2 グラフ 問題
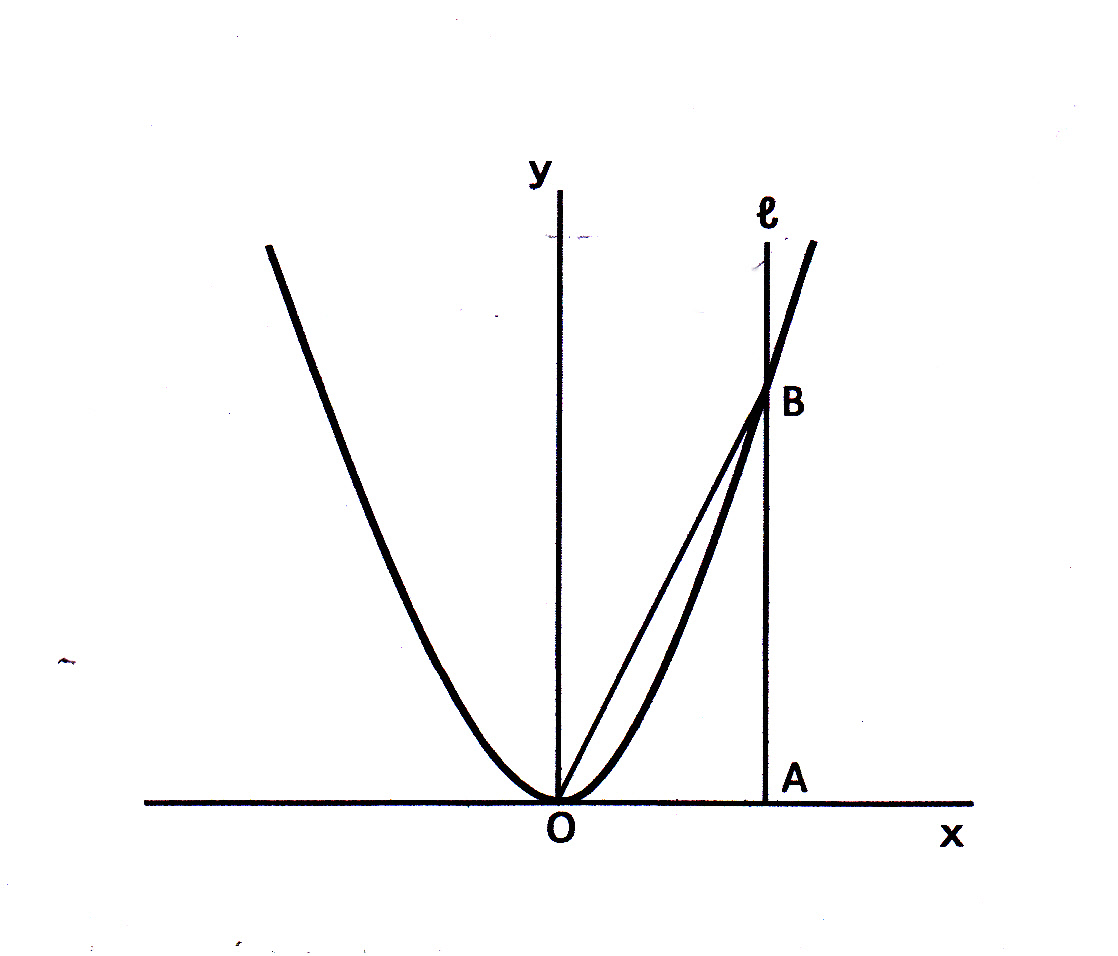
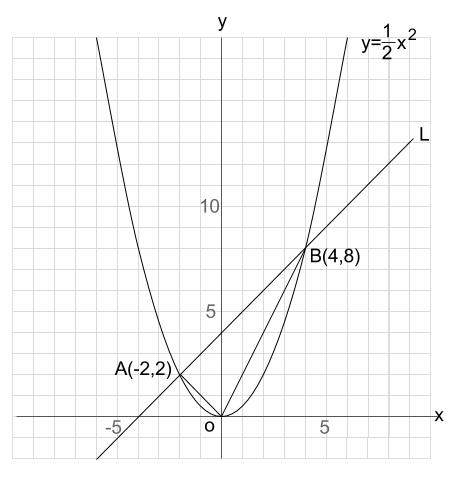
Y=ax2 グラフ 問題-そうすると,2次関数 y = ax2 + bx + c のグラフと x 軸の共有点の x 座標は,2次方程式 ax2 + bx + c =0の解であることがわかりますね。 それでは,これで回答を終わります。 これからも,『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。2 のグラフ1 4解説 4 図の放物線lはy=x2、 放物線mはy= 1 4 x2、 放物線nはy=ax2のグラフである。 それぞれの放物線と直線y=4との交点をA,B,Cとする。 AB=BCのときのaの値を求めよ。 y=4 x y l m n O A B C 点Aのx座標 4=x 2 より x=2




Y Ax 2 Cのグラフ 数学i フリー教材開発コミュニティ Ftext
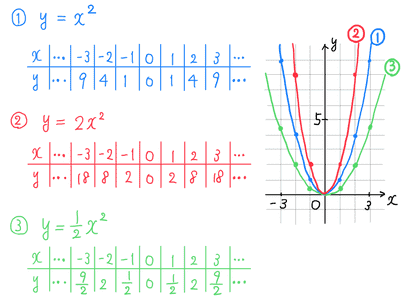
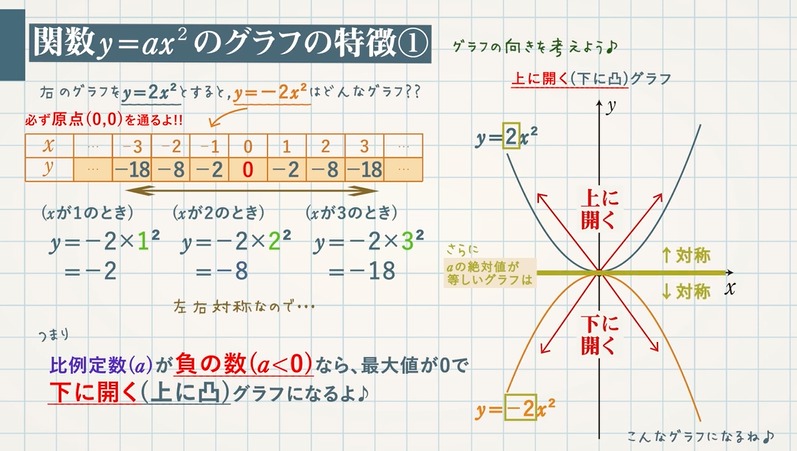
は曲線ですが、 上記の式は曲線にも使えるので、 気にする必要はありません。 簡単に計算できますよ! たとえば、 ★ y=2 x²117 rows関数 y=ax 2 (2) 関数 y=ax 2 のグラフ(1) 関数 y=ax 2 のグラフ(2) 関数 y=ax 2 のグラで、 変化の割合を求めるときに、 便利な公式なんです。 基礎を理解してから使えば、 速く解ける からです。 参考書には、おそらく 次のように書かれていたでしょう。関数y=ax²
北海道だと中々見る機会無いですからね。 そんな中,筑駒(高校入試)の,関数良問を発見。 筑駒らしく難易度は高いですが,裏技(クロスチョップ,サラスの公式)を知っていても有利にはあまりならない,そんな問題。 (2)までは,一般的な中学生において、 xの値が pからqまで 増加するとき、 変化の割合はY=ax2乗のグラフで覚えておきたい用語 まず、グラフの形は 放物線 となります。 この放物線は左右対称の形となっており、その折れ目となる線のこと
数学 1節 関数y=ax2 1) 関数y=ax2 数学 2節 関数y=ax2の性質と調べ方 2) 関数y=ax2 の値の変化 数学 3節 いろいろな関数の利用 1) 関数y=ax2 の利用・y=ax2q のグラフ ↓→例題 ↓y=ax2q のグラフy=ax2q のグラフを y=ax2 のグラフと比較しながら考えてみます。やはり表を作ってみることが大切です。 下の表は 2x2 と 2x21 を比較したものです。 xのどの値においても, 2x21 の値は 2x2 の値に1を足したものです。したがって, y=2x21 のグラフは y=2x2ここでは,関数y=ax2 のグラフとその特徴について学習してみましょう。 関数y=ax2 において,x=k,-kのときのyの値をそれぞれ求 めると,ともに y=ak2, ya k ak=-=_i2 2 となるから, y=ax2 のグラフは 軸に関して対称であるといえます。



2



ベスト Y Ax2 グラフ シモネタ
\(y=ax^2\)という形をした関数のグラフは このような 放物線 と呼ばれるグラフになります。 放物線というワードは定期テストで問われることもあるから覚えておこう!学習しました 中3数学「関数 = y = a x 2 のグラフ 変域 変化の割合」の問題 どこよりも簡単な解き方・求め方 前回、新しく「2乗に比例する関数」を学習しました 今回は関数と言えば「グラフ」「変域」「変化の割合」です では、一緒に見ていきA,Bの座標が次のそれぞれの場合において、y=ax 2 のグラフが線分AB(両端を含む)と交わるようなaの値の範囲を求めよ。 A(2,1), B(2,8) A(4, 4), B(4, 8) A(3, 1), B(3, 9) 図の放物線lはy= 1 2 x 2 の グラフで、放物線mはy=ax 2 のグラフである。lとmがx軸に平行な直線nと交わる点をそれぞれA, Bとする。Aのx座標が



2次関数の基本



二次関数のグラフの書き方
例1 y=x 2 のグラフ上に2点A,Bがあります.A,Bの x 座標がそれぞれ −1, 3 であるとき,次の問いに答えなさい. (1) 2点A,Bの座標を求めなさい. (2) 2点A,Bを通る直線の方程式を求めなさい. (3) 2点A,Bを通る直線が y 軸と交わる点Pの座標を求めなさい.関数グラフ GeoGebra x y z π 7 8 9 ×二次関数y=ax2のグラフの書き方がわかる 3つのステップ 二次関数y=ax2のグラフの書き方はつぎの3ステップ。 点をたくさんゲット;




Y Ax 2 Bx C のグラフのかき方 事前テスト解答例 Kyokuryo Math




Y Ax 2 Bx Cのグラフ 数学i フリー教材開発コミュニティ Ftext
関数y=ax2の関 係などを,表,式,グ ラフを用いて的確に表 現したり,数学的に処 理したりするなど,技 能を身に付けている。 事象の中には関数y =ax2などとして捉 えられるものがあるこ とや関数y=ax2の 表,式,グラフの関連と呼びます。 さて,ここまであつかった2次関数は,y=ax2 という形をしていましたが,ここで,y=ax2 をもっと一般的な形,つまり y=ax2bxc へ拡張し,今後,この形のグラフや性質について調べていくことにしましょう。 そこで,次のような目的に基づいてその上でy=xに対称な点や,中点の扱い,また公立高校でも使えそうなテクニック等,色々学べます。 この問題,1つ1つの知識はそこまで難しくないです。 それが何個も組み合わせると難関。 何となくですが,灘は,中学入試はもちろんえげつない難易度。 しかし,高校入試はある程度努力で何とかなりそうですね(とはいえ難しい)。 中学入試は特別な訓練と




Y Ax 2 Cのグラフ 数学i フリー教材開発コミュニティ Ftext




Y Ax 2 Bx C のグラフのかき方 事後テスト解答例 Kyokuryo Math
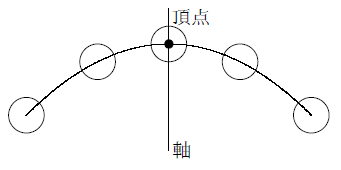
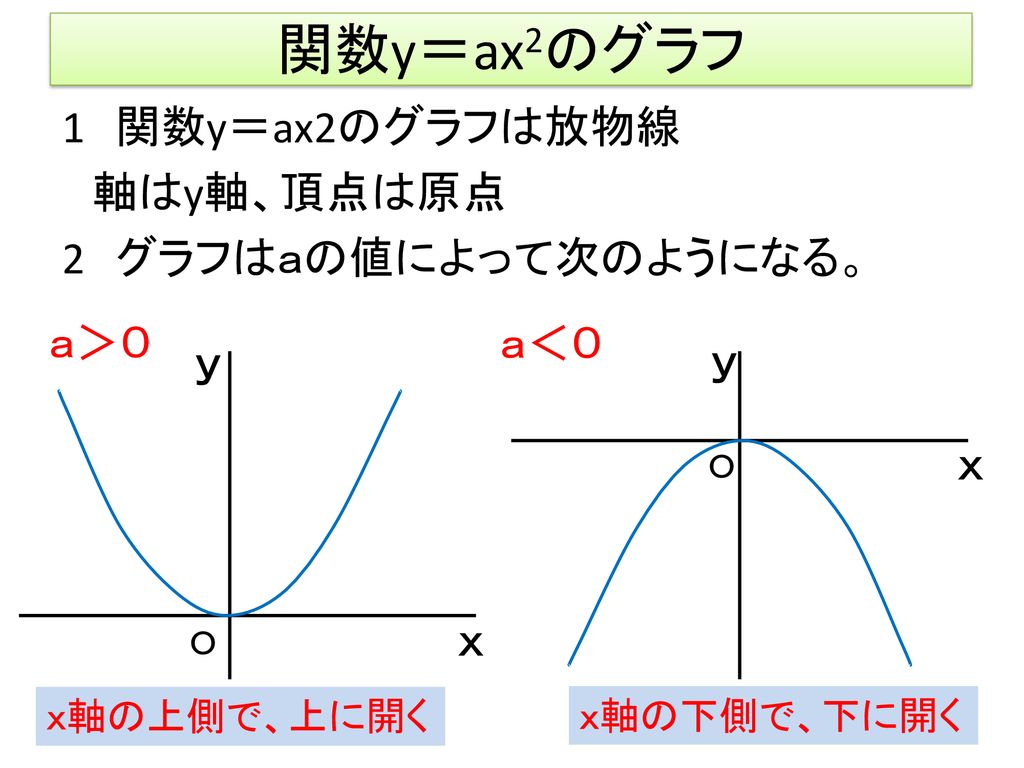
Y=ax 2 (a>0)のグラフは、図のように 「原点を通る、上に開いた放物線」 になるよ。 U字型 のイメージだね。 例題をいっしょに解きながら、実際にグラフが 「原点を通る、上に開いた放物線」 になることを確認していこう。2次関数y=ax^2のグラフのポイントは! 原点を通る y 軸に対称 y=ax^2のグラフの形を「放物線」という 放物線の尖がっている先っちょを「頂点」と(yの増加量)÷(xの増加量) という割り算で求められます。 ( "割り" あいなので、 割り算 ですね!) y=ax²




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ




二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ
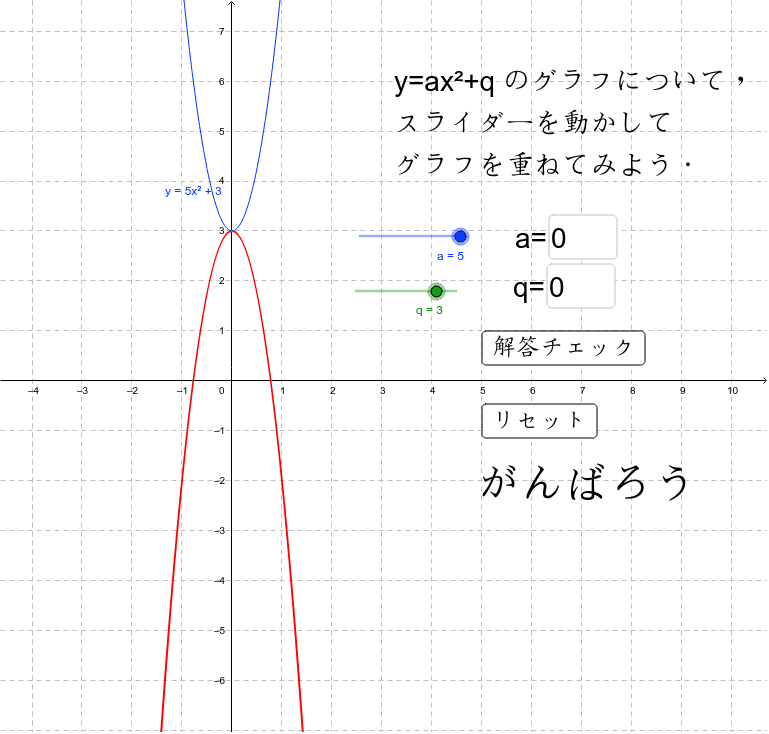
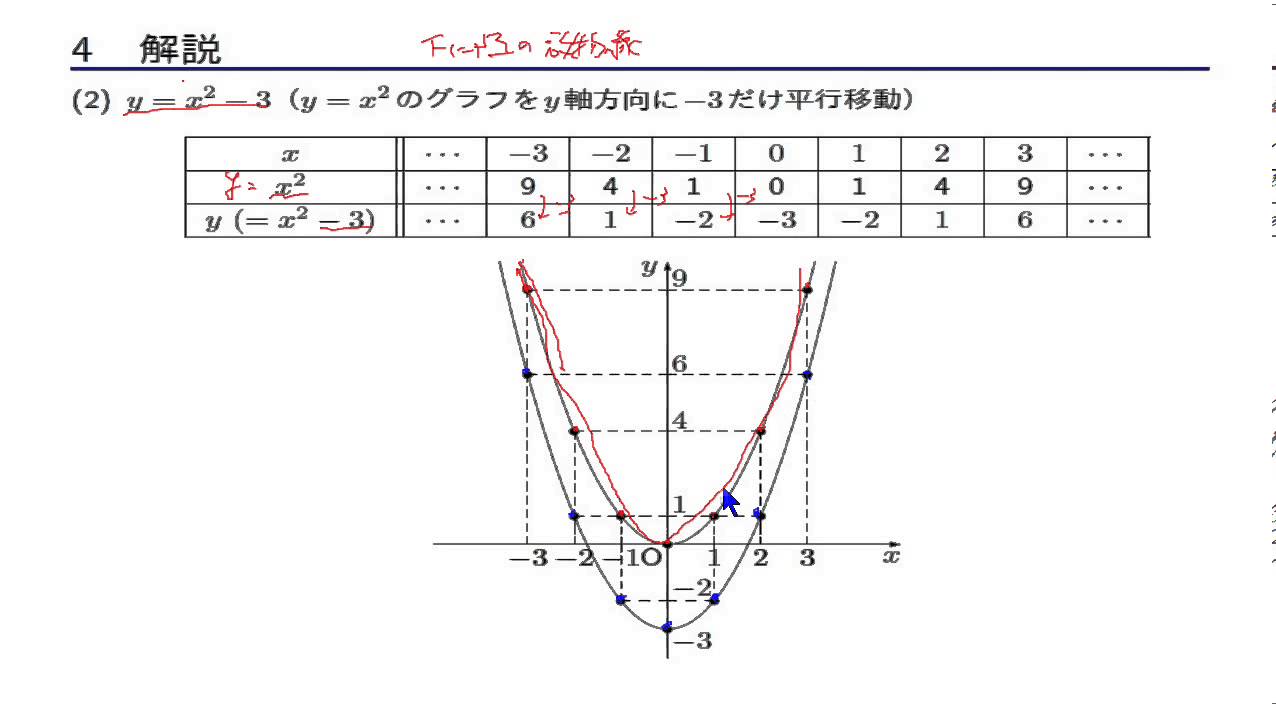
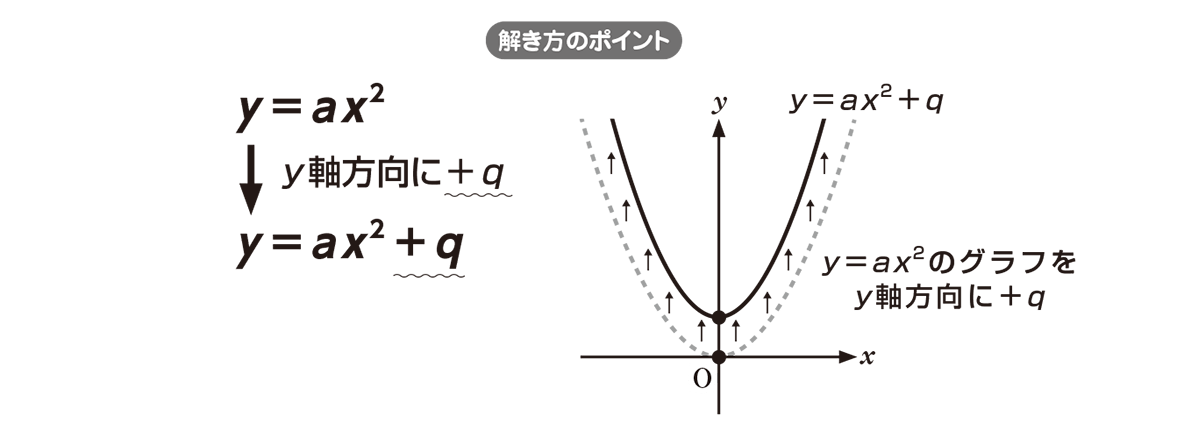
$y=ax^2q$ のグラフは、 $y=ax^2$ のグラフを y 軸方向に q だけ移動したものである 基本二次関数 y=ax^2 のグラフ では、放物線の頂点と軸の紹介をしました。なぜなら、一次関数y=axbでbが0のときの場合にすぎないからね。 xの2乗に比例する関数のあつかいも、 比例と一次関数の関係に似ていると思っておこう。 まとめ:関数y=ax2は二次関数の仲間! 関数y=ax2を二次関数とよんでしまうのは、Y=ax 2 のグラフ 2次関数とは、y=2x 2 y=ax 2 bxc 中学校では、b=0,c=0 の場合だけ扱い、関数y=ax 2 のグラフが放物線という曲 線になっていることを勉強しました。



数学の問題です 図のように関数y Ax2 2乗 のグラフ上に3点a B Yahoo 知恵袋



2次関数の基本
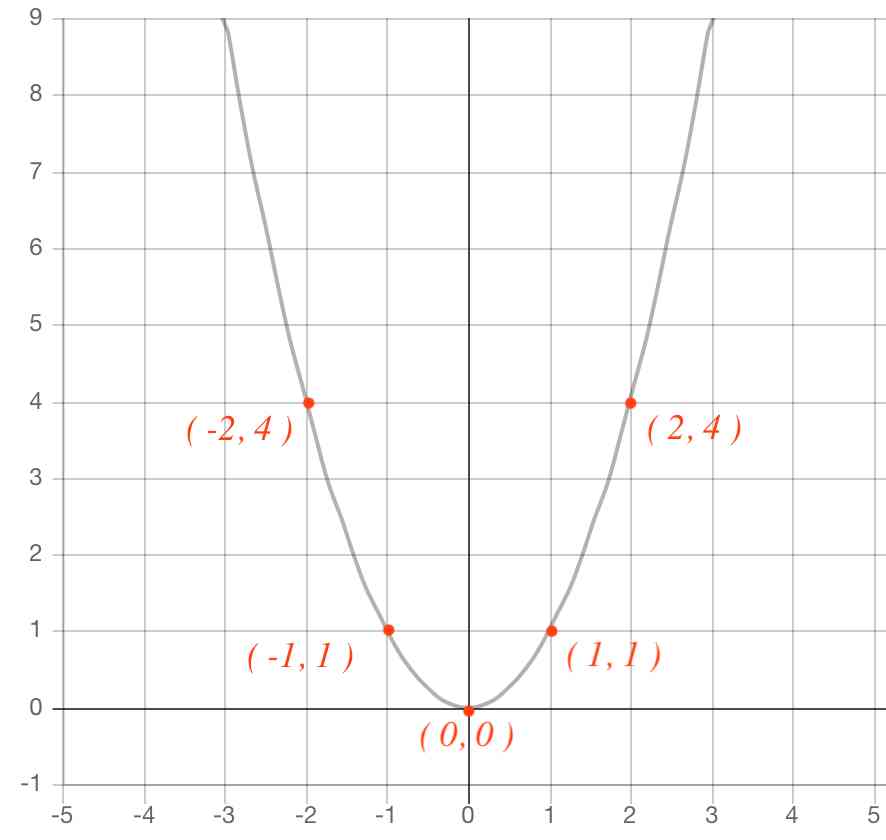
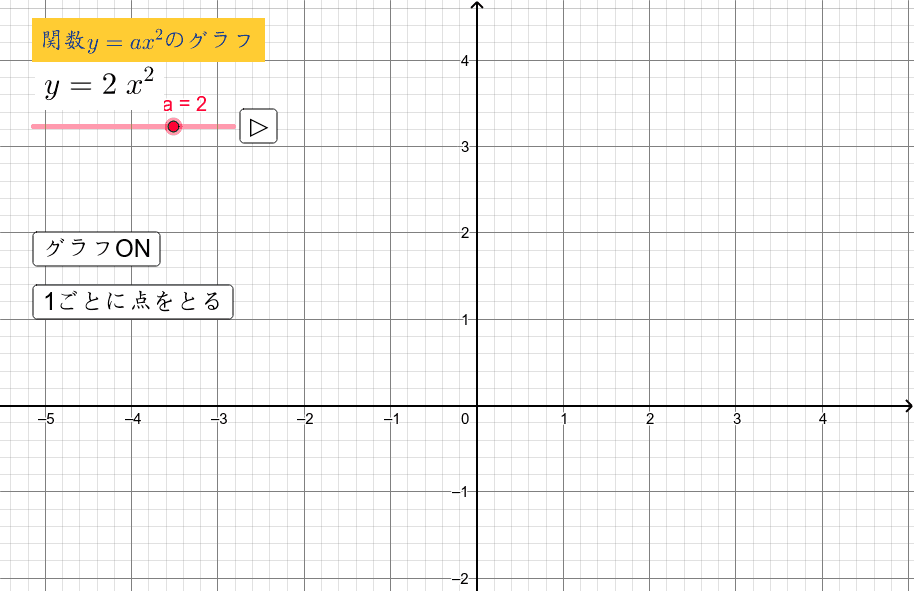
時間xと距離yの関係を一次関数や関数y=ax2 で近似し,グラフ描画ソフトやグラフ電卓を 図1 提示する問題 藤原大樹(16)「複数のICT を活用した関数領域における数学的モデリング」,東京理科大学数 学教育研究会「数学教育」第58 巻第1 号,pp1151.関数y=ax 2 のグラフ 解説 まずは,関数y=ax 2 のグラフの基本となる,a=1のときのグラフ,つまり,関数y=x 2 のグラフについて考えていきます。 グラフをかくには, xとyの対応表を完成させる。 1の表から,それらに対応する点(x,y)を図にかき入れ,その点をなめら↑ 反比例のグラフ ( 双曲線 ) ↑ y=ax2 のグラフ ( 放物線 ) また、それぞれの関数の式は決まっていますよね? 比例 → y = ax 一次関数 → y = axb 反比例 → y = a/x 関数 y=ax2 → y = ax2 (aやbには、具体的な数が入ります)



1 2次関数のグラフ ノート ひまわり数学教室




2番の解き方を教えてください お願いします Clearnote
Y = a x 2 の関係にある2量に着目し、関数的な考え方を進んで活用しようとする 式、値の変化、グラフなどから関数関係を分析し、その特徴を理解し、問題を関数的に解決する y = ax2 y = a x 2 の関係にある数量を、表、式で表したり、変数の変域、



Y Ax 2



関数y Ax2のグラフ まなびの学園



05 01関数のグラフで理解しておきたいところ
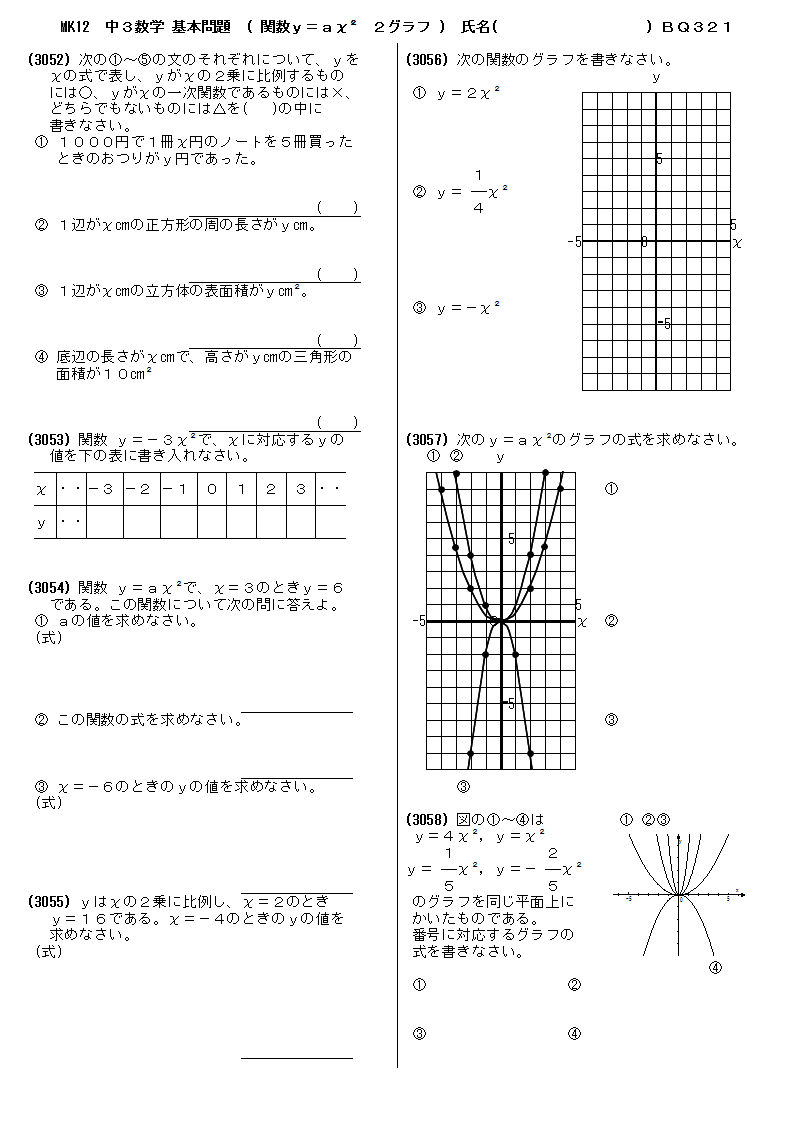



無料 中3数学 基本問題 問題プリント 321 関数y ax2 2グラフ



栃木県総合教育センター 算数 数学 学びの杜 中学校3年生 数学 関数y ax 2のグラフ




2次関数のグラフ



関数y Ax2乗グラフ利用の問題が分からないため 解説付きで教えて下さ Yahoo 知恵袋



Y Ax 2




勉強しよう数学0 2次関数のグラフの平行移動




中3数学 Y Ax 2のグラフ A 0 映像授業のtry It トライイット




最高のy Ax2 グラフ 書き方 最高のカラーリングのアイデア
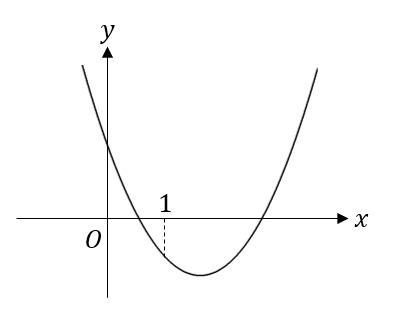



二次関数 係数の符号の決定 グラフから符号を決めるポイントを解説 数スタ




2次関数のグラフと方程式
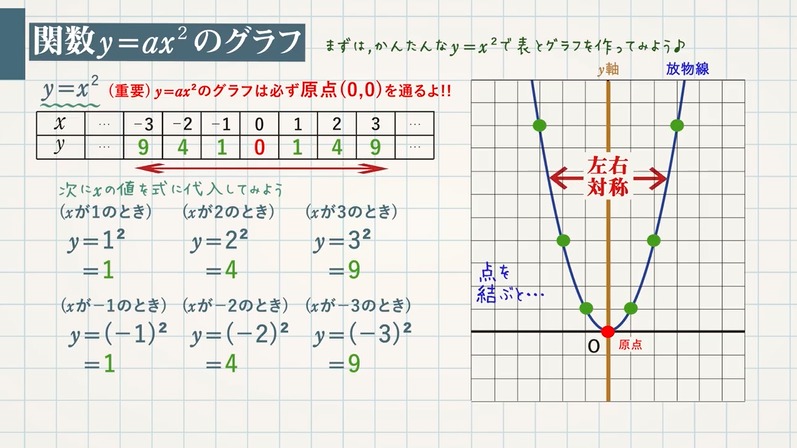



関数y Ax のグラフの性質 教遊者



2乗に比例するグラフ 中学から数学だいすき




2乗に比例する関数のグラフ 放物線 の書き方 無料で使える中学学習プリント




二次関数 Wikipedia
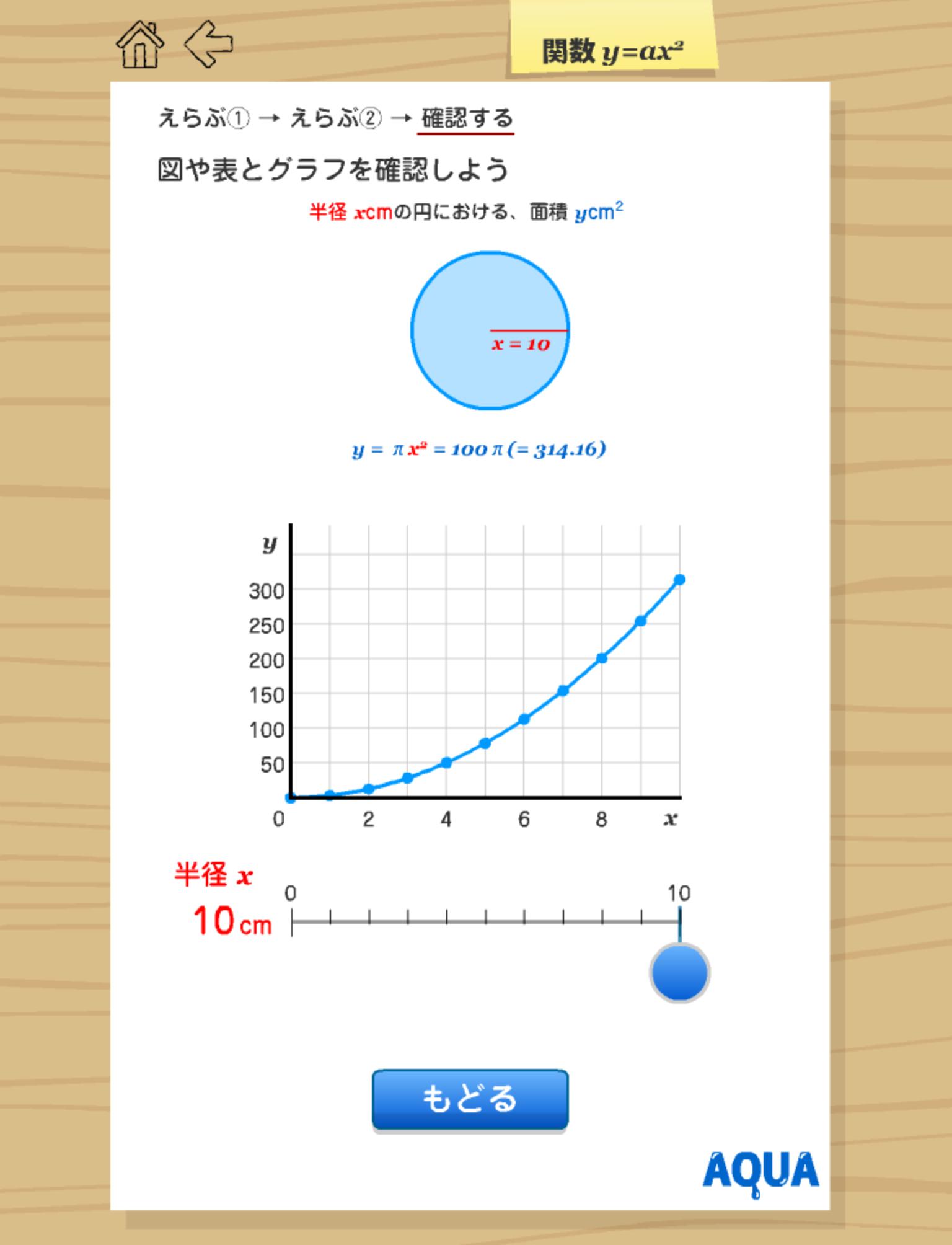



関数y Ax2 さわってうごく数学 Aquaアクア For Android Apk Download



関数y Ax2のグラフ さわってうごく数学 Aquaアクア Androidアプリ Applion



1
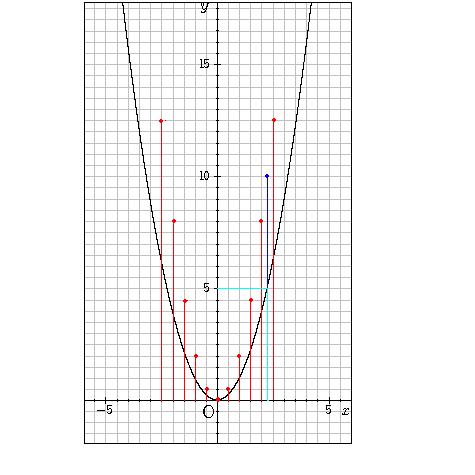



Y 2x 2のグラフ Takapの数学日記




二次関数のグラフの問題 aの値で上か下かの向きが決まるよ 中学や高校の数学の計算問題
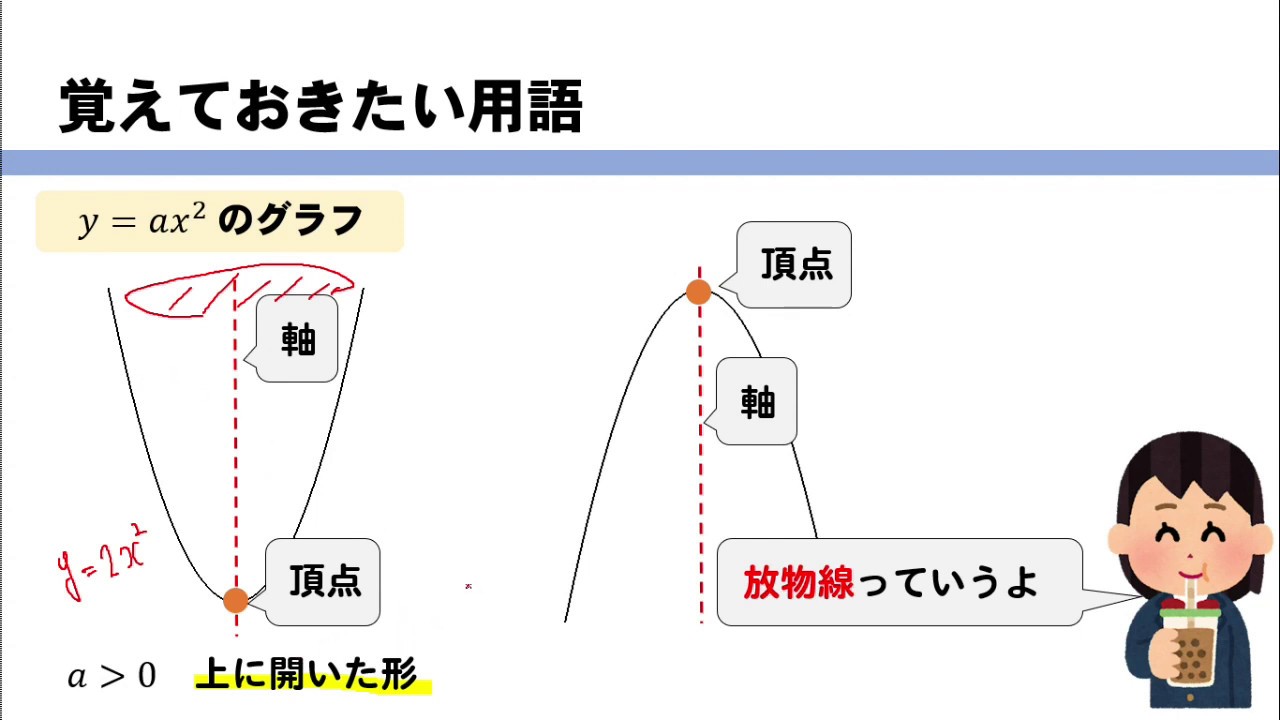



Y Ax2乗 グラフの特徴と書き方をイチから解説します 中学数学 理科の学習まとめサイト
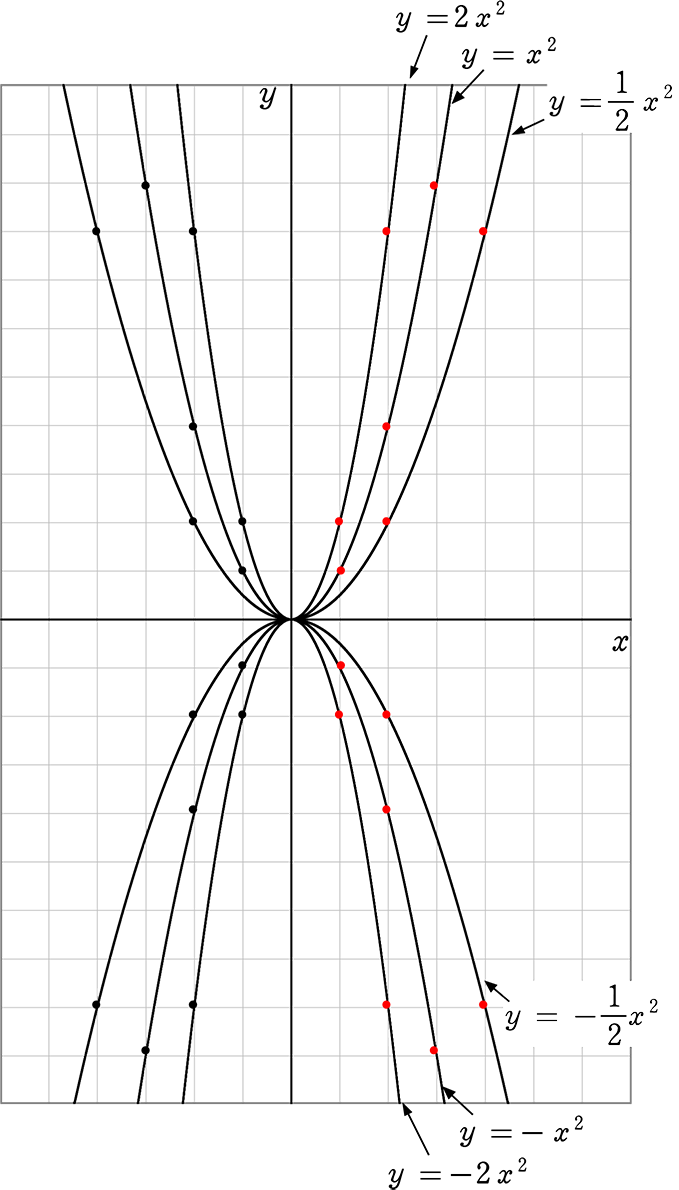



中学数学 関数
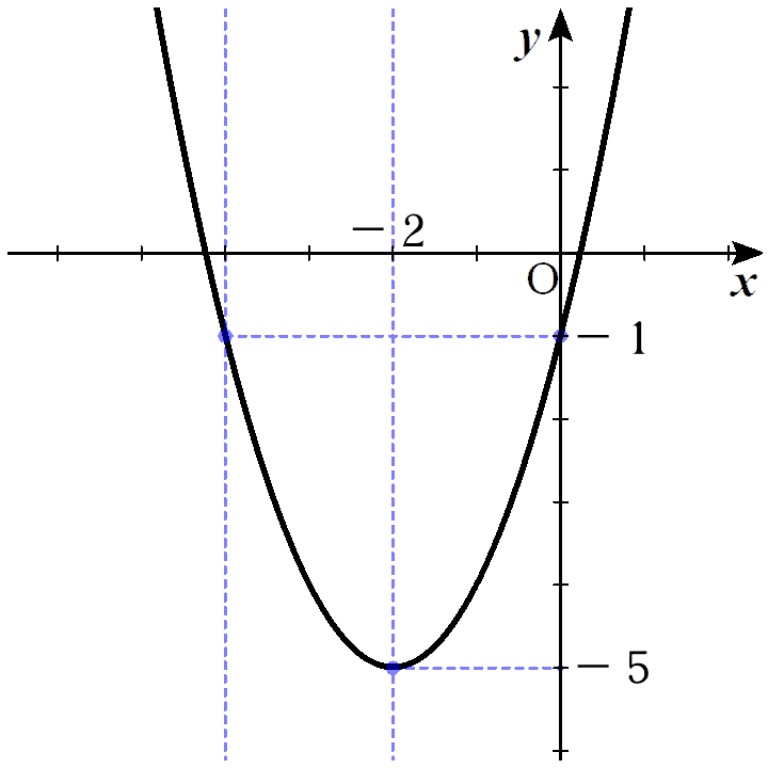



Tossランド 関数とグラフ のコンテンツ集




例題で学ぶ高校数学 Y Ax2 Q




数学3年 2次関数 Y Ax2 2次関数のグラフ 2次関数の変域 2次関数の応用 2次関数のグラフ Xの2乗に比例する関数 問題1 正解1 解説1 問題2 正解2 解説2 問題3 正解3 解説3 問題4 正解4 解説
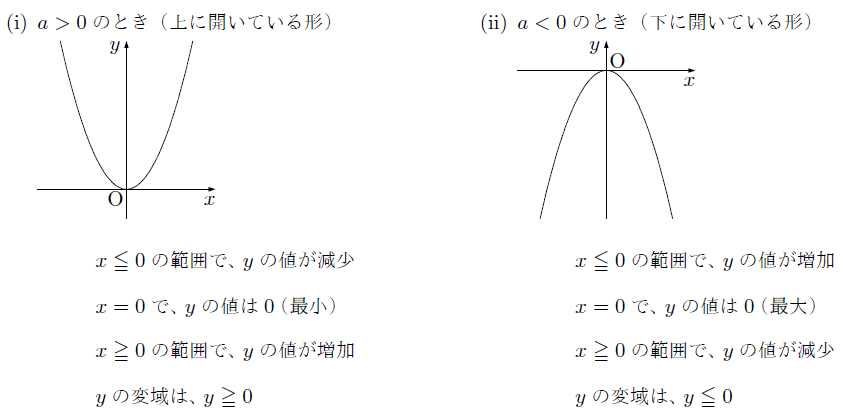



関数の変域 まなびの学園




基本 二次関数 Y Ax 2 のグラフ なかけんの数学ノート
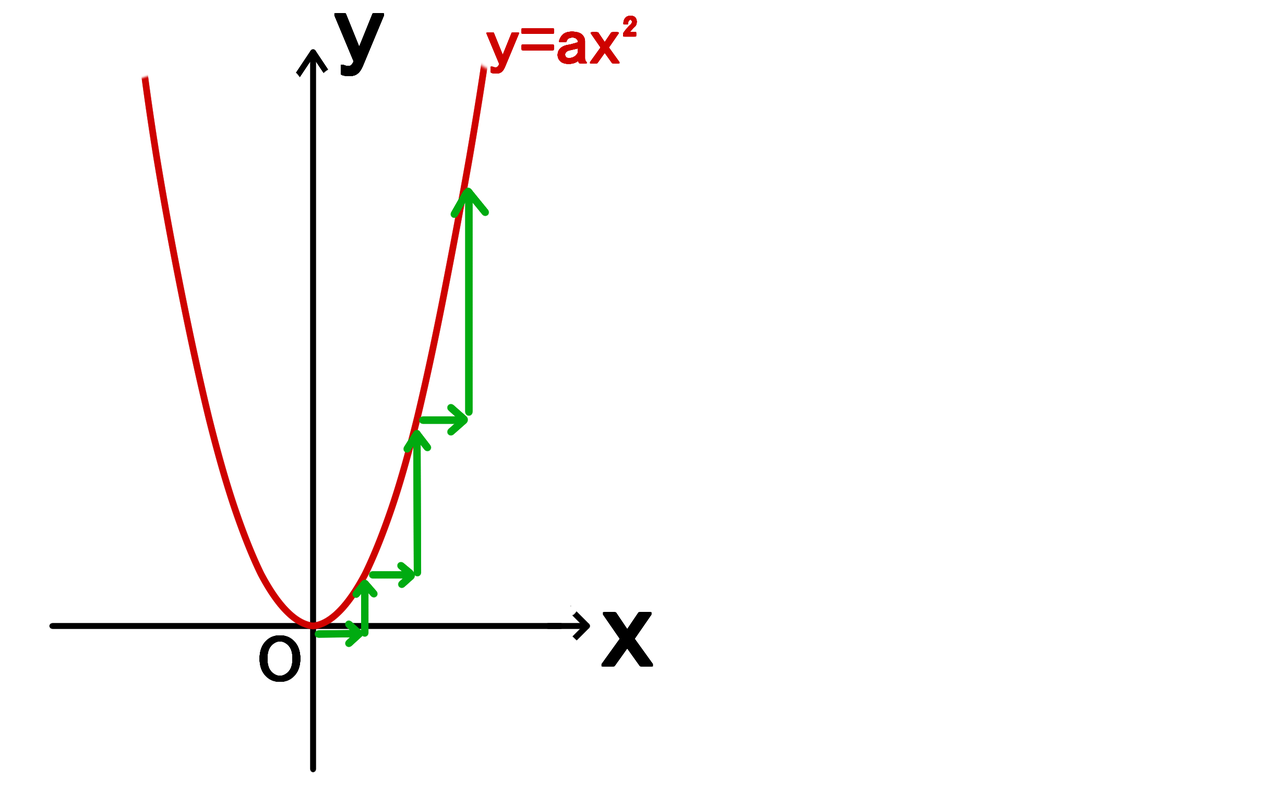



関数y Ax の 変化の割合 の問題 Xの値がaからa 2まで増加したときに Yの値は バカでもわかる 中学数学
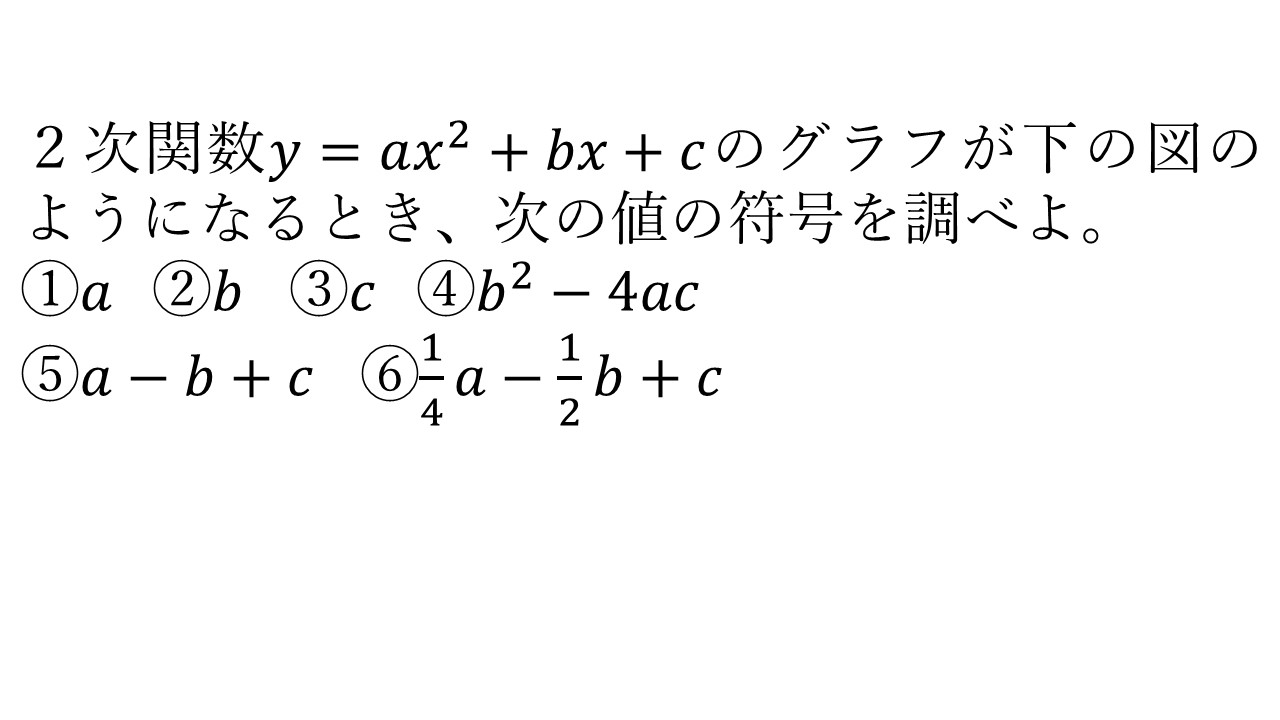



二次関数のグラフから係数の符号を調べる 大学受験の王道



1
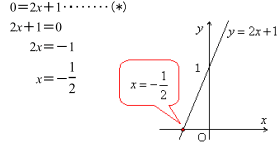



2次関数のグラフとx軸の共有点 と 2次方程式の解 数学 苦手解決q A 進研ゼミ高校講座




Y Ax Bのグラフと 切片と傾きの意味 中学数学 By じょばんに マナペディア




高校数学 Y Ax 2のグラフ 下に凸 上に凸 映像授業のtry It トライイット



関数y Ax のグラフの性質 教遊者



中学数学 3年 教育出版




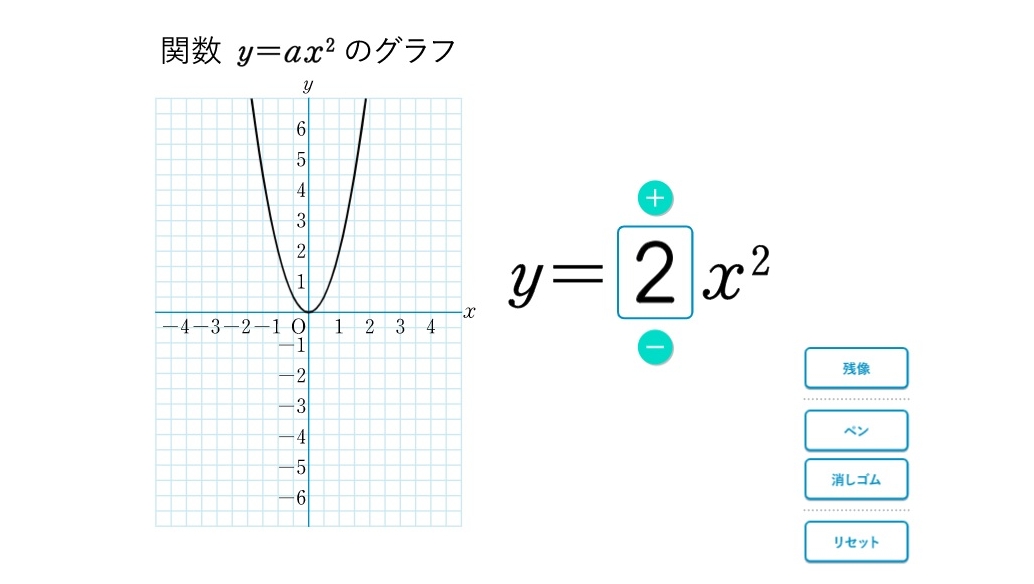
二次関数y Ax2の放物線にみられる5つの特徴 Qikeru 学びを楽しくわかりやすく
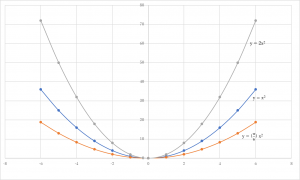



Y Ax2 おやじさん ネット




高校数学 Y Ax 2 Bx Cのグラフ 例題編 映像授業のtry It トライイット
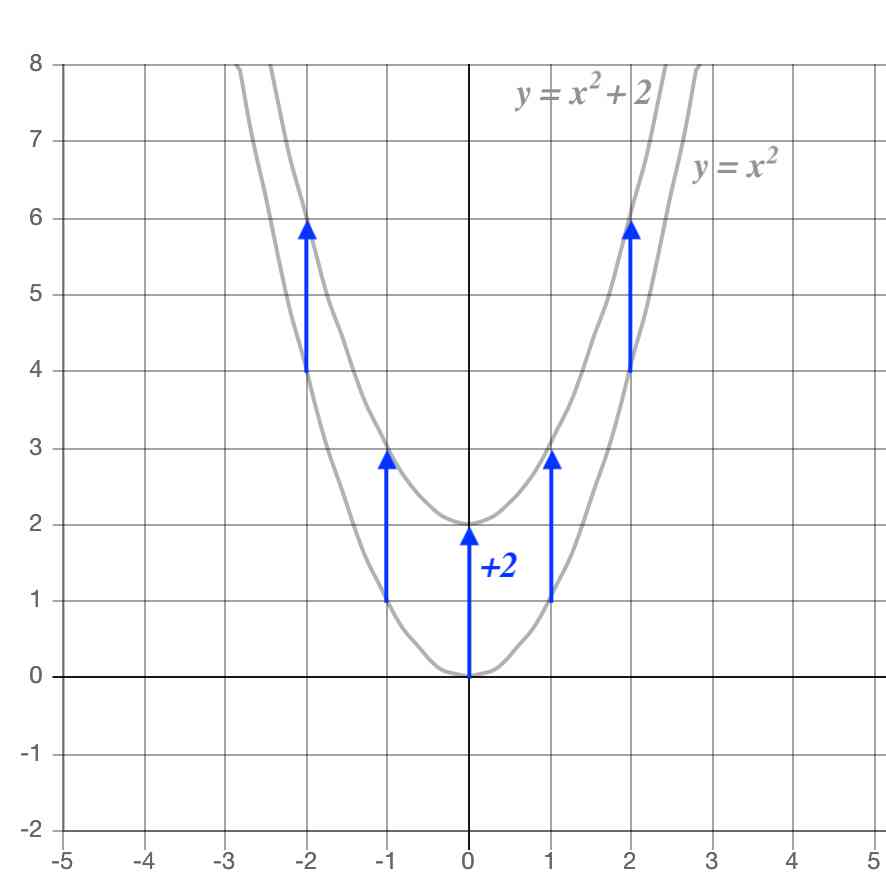



二次関数のグラフの書き方



2




Y Ax2乗の利用 放物線と直線による面積 中学3年の問題をイチから解説 中学数学 理科の学習まとめサイト



Y Ax のグラフ 中学3年 数学クラブ
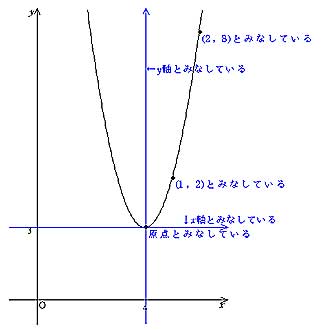



授業実践記録



二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師



年前期 千葉県公立高校入試前期 数学 第2問 1 Y Ax2の変域 問題 解答 解説 動画解説 文字解説両方あり 船橋市議会議員 朝倉幹晴公式サイト




関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ




y が x の2乗に比例する関数のグラフ 算数 数学が好きになりmath



下に凸の放物線 Y A X 2 A 0 のグラフ 数学をもう一度




2次関数のグラフと直線
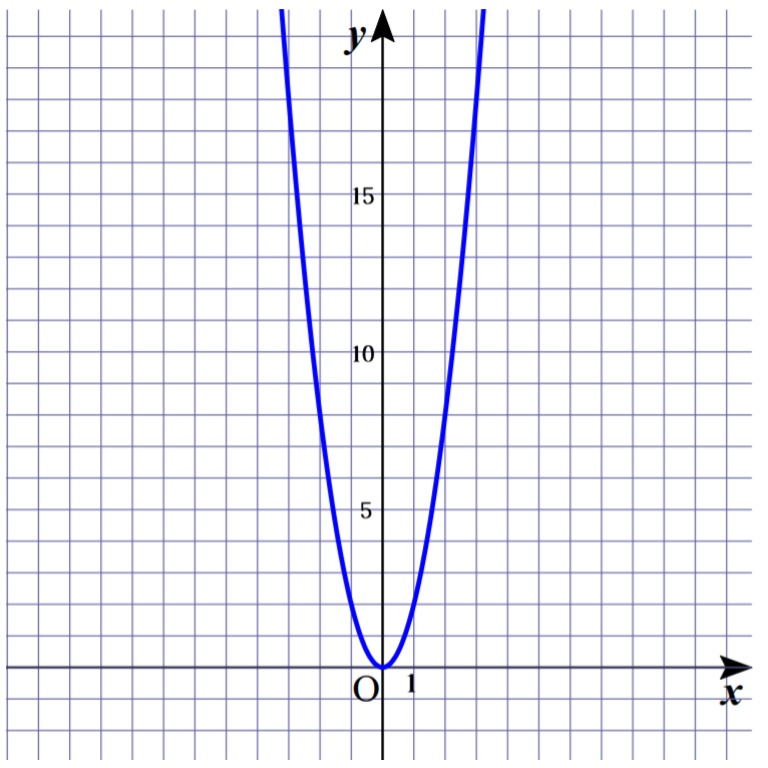



Tossランド マス目があるグラフ Y 2x2 Dl可
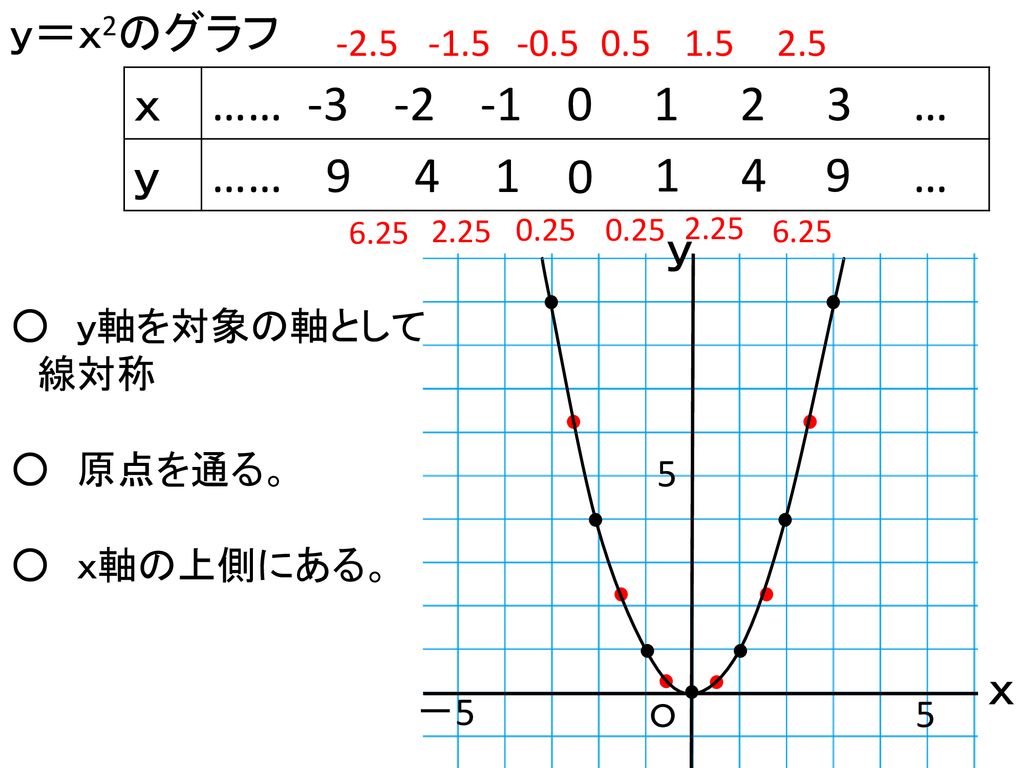



ねらい 関数y ax2のグラフをかき その特徴を理解する Ppt Download




関数y Ax2乗のグラフの書き方を教えてください ཀ Clearnote



Y Ax 2 Qの関数のグラフの形 Geogebra



y ax 2のグラフ2



二乗に比例とは 1分でわかる意味 式 グラフ 例 比例との違い



ねらい 関数y ax2のグラフをかき その特徴を理解する Ppt Download



二次関数の利用の問題の解き方 グラフの問題 1 現役塾講師のわかりやすい中学数学の解き方




中学数学 二次関数y Ax2のグラフから式を3秒で読み取る方法 Qikeru 学びを楽しくわかりやすく



関数y Ax 2のグラフ Geogebra




中3 Y Ax二乗のグラフの性質 変域の求め方 中学生 数学のノート Clearnote




例題で学ぶ高校数学 Y Ax2
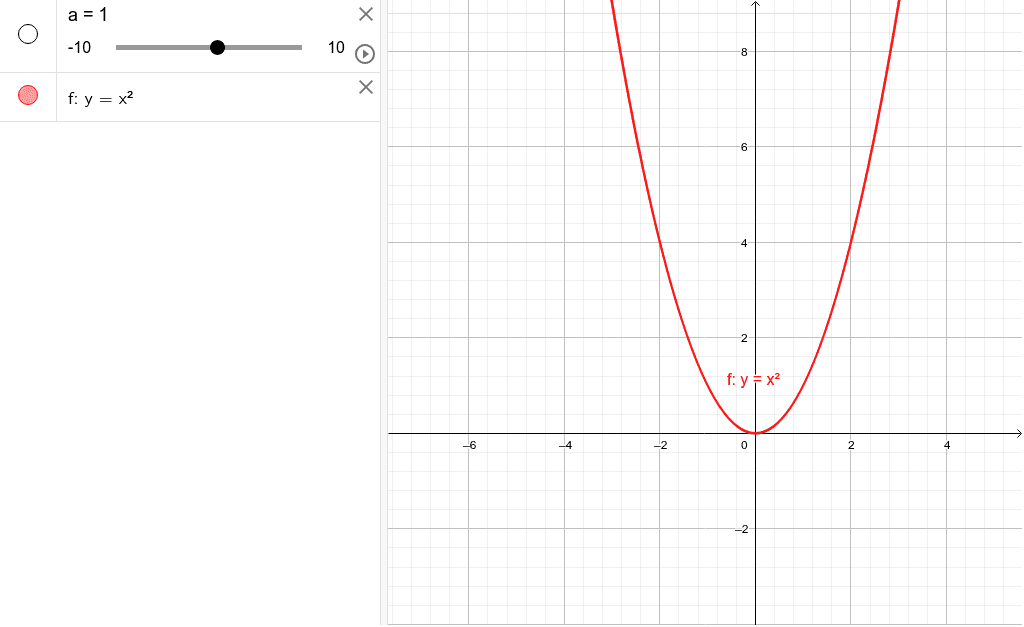



Y Ax 2のグラフ Geogebra




中学数学 二次関数y Ax2のグラフの書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



2
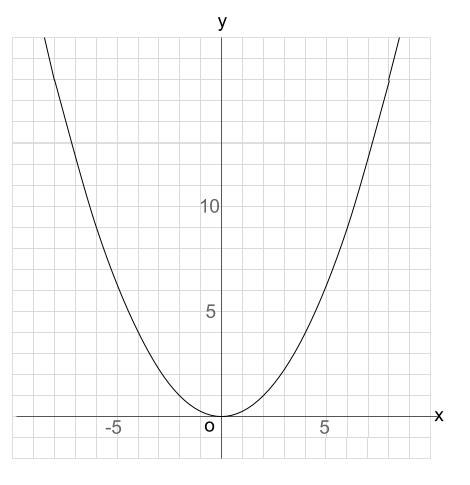



中学数学 Y Ax 2 のグラフを読み取る 中学数学の無料オンライン学習サイトchu Su




Y Ax 2の変域 チーム エン
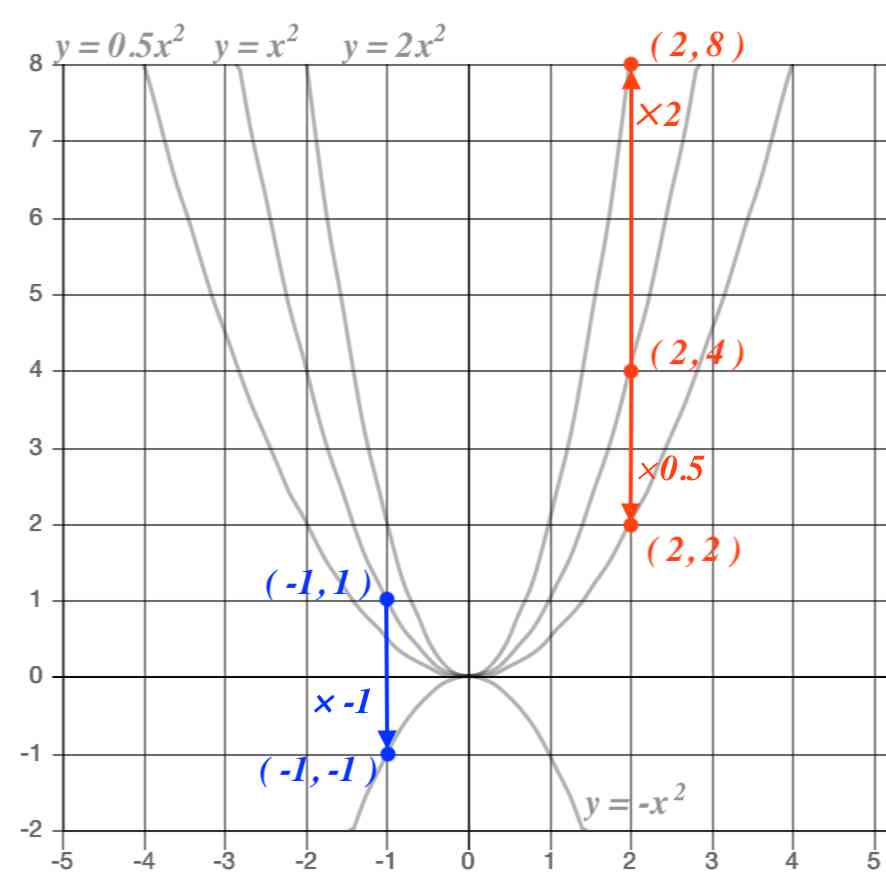



二次関数のグラフの書き方




Y Ax2乗 Aの求め方についてパターン別に解説 発展問題もアリ 中学数学 理科の学習まとめサイト
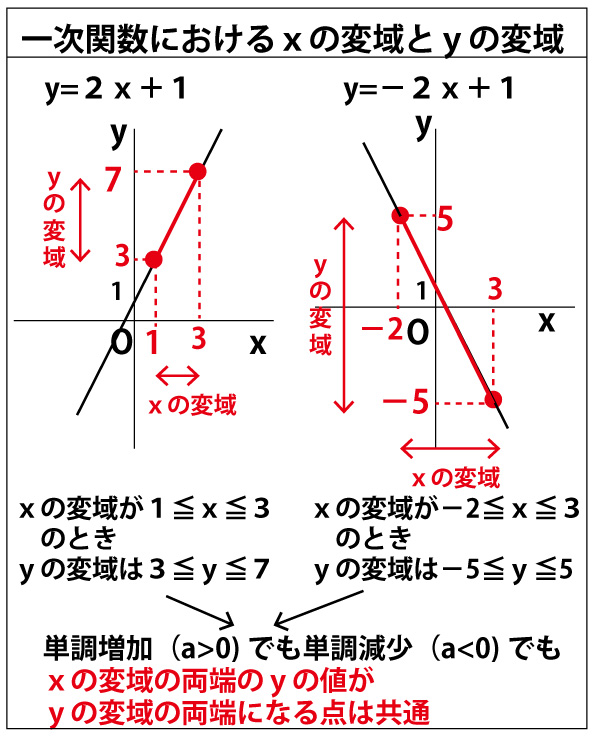



年前期 千葉県公立高校入試前期 数学 第2問 1 Y Ax2の変域 問題 解答 解説 動画解説 文字解説両方あり 船橋市議会議員 朝倉幹晴公式サイト




中学数学 二次関数y Ax2のグラフから式を3秒で読み取る方法 Qikeru 学びを楽しくわかりやすく




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ




二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ




関数y Ax2乗 変域の求め方 変域から式を求める問題を解説 Youtube



2次関数のグラフ Y Ax 2



中学数学 Y Ax 2 図形との融合問題 中学数学の無料オンライン学習サイトchu Su




ベストコレクション Y Ax2 グラフ 書き方 ニスヌーピー 壁紙
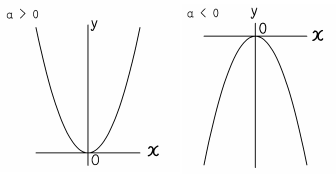



2乗に比例する関数 グラフ



数学i 2次関数 2 2 Y Ax 2 Qのグラフ Youtube



1




スタディピア 関数とグラフ




2次関数y Ax のグラフとは バカでもわかる 中学数学



関数y Ax2乗 問題



高校数学 Y Ax 2 Qのグラフ2 映像授業のtry It トライイット




Y Ax 2 Bx Cのグラフ 数学i フリー教材開発コミュニティ Ftext
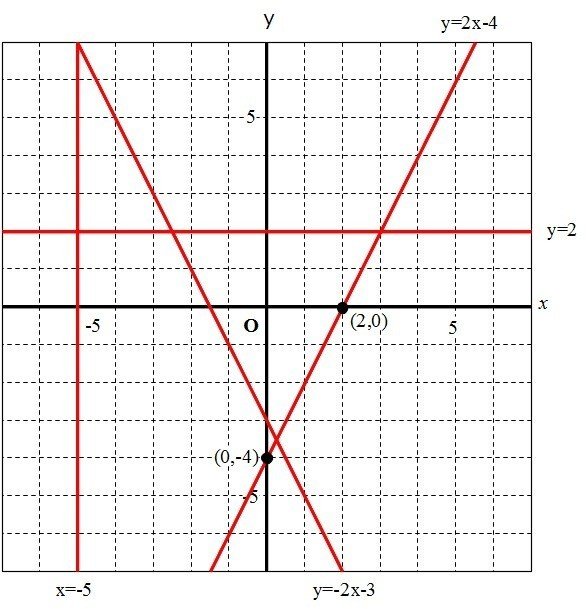



超速まとめ 一次関数 一次関数の式 変化の割合 グラフ 二元一次方程式 Shun Ei Note




3年 関数 Y X のグラフ 数学イメージ動画集 大日本図書
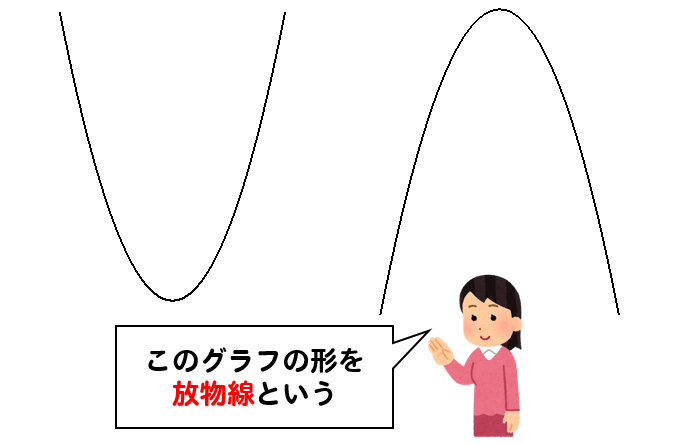



関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ
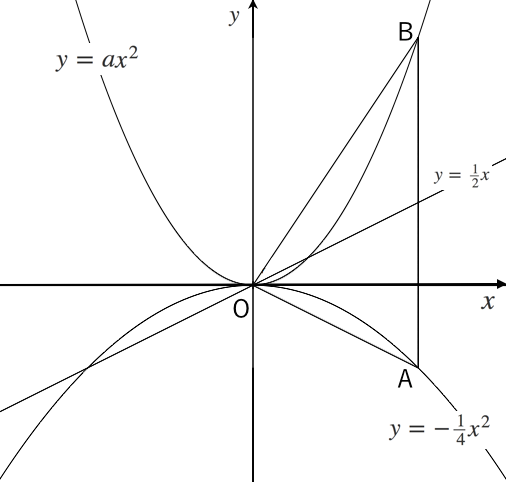



二次関数の利用 グラフ系の問題 苦手な数学を簡単に

コメント
コメントを投稿